1量子ビットの反転誤りの訂正

量子誤り訂正の中でも一番簡単な1量子ビットの反転誤りを訂正する方法について考える。ビット反転誤りとは
\begin{equation}
\Ket{0} \rightarrow \Ket{1} , \quad \Ket{1} \rightarrow \Ket{0}
\end{equation}
となる誤りのことを言う。これを訂正する方法を考える。

古典ビットの誤り訂正では冗長性を使っていた。つまり1ビットの0を例えば3ビットの000にコピーして、多数決をとって多い方を元のビットと考える。量子ビットの訂正でも同じ方法をとりたいが、量子系では複製禁止定理からコピーをとることは禁止されている。また量子系では測定によって状態が変わってしまうことにも注意する必要がある。

まず複製禁止定理から任意の状態$\Ket{\psi}$をコピーする操作
\begin{equation}
\Ket{\psi} \Ket{0} \rightarrow \Ket{\psi} \Ket{\psi}$
\end{equation}
は許されない。しかし任意ではなくある決まった1つの量子状態$\Ket{\psi}$をコピーする操作は許される。
そこで計算でつかう1つの量子ビット（論理ビットという）を3つの物理的な量子ビットで表現する。つまり
\begin{equation}
\Ket{0_L} = \Ket{000} ,\quad \Ket{1_L} = \Ket{111}
\end{equation}
とする。論理ビットが物理ビットかを区別するために、論理ビットには$L$の添え字をつけている。重ね合わせ状態にある論理量子ビットは
\begin{equation}
\Ket{\psi_L}= \alpha \Ket{0_L} + \beta \Ket{1_L}
\end{equation}
とする。この状態は$
\Ket{\psi}= \alpha \Ket{0} + \beta \Ket{1} $のコピーでないので、量子複製禁止定理に抵触しない。重ね合わせ状態にある論理ビットの状態を作るには
以下の回路を使えば良い。

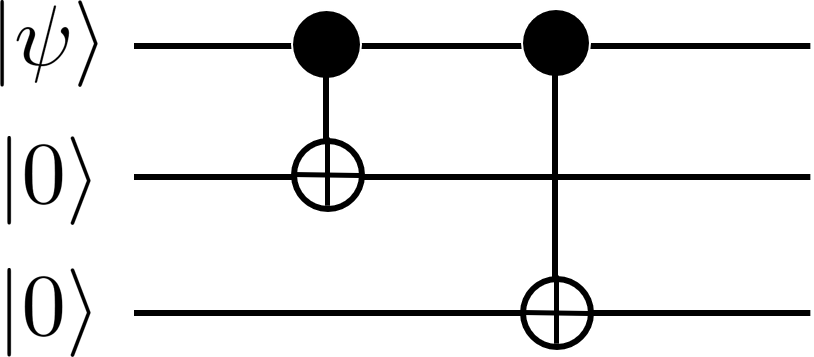
この回路で重ね合わせ状態の論理ビットが作れることは
\begin{eqnarray}
(U_{CNOT,1,3} \otimes I_2)(U_{CNOT,1,2} \otimes I_3) \Ket{\psi} \Ket{0} \Ket{0} &=&
(U_{CNOT,1,3} \otimes I_2) (\alpha \Ket{0} \Ket{0} \Ket{0} + \beta \Ket{1} \Ket{1} \Ket{0} \\
&=& \alpha \Ket{000} + \beta \Ket{111}
\end{eqnarray}
から確かめられる。

以下では3量子ビットのうち、反転誤りを起こすのは多くても1つの量子ビットとする。このとき、考えられる状況は、誤りなし、1つめの量子ビットが反転、2つめの量子ビットが反転、3つめの量子ビットが反転の4通りである。

誤りがない場合はすべての量子ビットは同じ状態にあるので、ビットが反転しているかどうかは、他の量子ビットと比べて同じ状態であるか否かを測定することで分かる。このためにパリティ測定という測定を行って反転誤りを検出する。

二つの量子ビットに対するパリティ測定演算子$P$は
\begin{equation}
P = (\Ket{00}\Bra{00} + \Ket{11} \Bra{11}) – (\Ket{01}\Bra{01}+\Ket{10}\Bra{10})
\end{equation}
で定義される。二つの量子ビットが$\Ket{00}$や$\Ket{11}$と同じときは$+1$の固有値を、$\Ket{10}$や$\Ket{01}$と異なるときは$-1$の固有値を返す演算子である。計算基底は$P$の固有状態なので、量子系の測定による状態変化の問題も回避できる。

第1ビットと第2ビットのパリティ測定$P_{12}$と第2ビットと第3ビットのパリティ測定$P_{23}$の二つの測定値は全部で4通りあるが、ちょうど誤りのパターンの4通りと対応する。対応表は以下の図の通りである。

二つのパリティ測定から誤りが特定できたら、最後は誤っている量子ビットにビット反転の操作である$X$ゲートを作用させれば誤り訂正ができる。