1量子ビットの位相誤り訂正

このページでは1量子ビットの位相誤りを訂正する方法を考える。位相反転誤りは
\begin{equation}
\Ket{0} \rightarrow \Ket{0}, \quad \Ket{1} \rightarrow -\Ket{1}
\end{equation}
となる誤りである。$\Ket{1}$のときは位相が$\pi$だけずれてしまう。

この位相誤りを訂正するための論理ビットの基底として
\begin{equation}
\Ket{0_L} = \Ket{+ + +} , \quad \Ket{1_L} = \Ket{- \ -\ -}
\end{equation}
を考える。ここで$\Ket{\pm}$は$X$ゲートの固有状態$\Ket{\pm} = \frac{1}{\sqrt{2}} (\Ket{0} \pm \Ket{1})$である。位相誤りをこの基底で表現すると
\begin{equation}
\Ket{+} \rightarrow \Ket{-}, \quad \Ket{-} \rightarrow \Ket{+}
\end{equation}
となる。
論理ビットの重ね合わせ状態
\begin{equation}
\Ket{\psi_L} = \alpha \Ket{+++} + \beta \Ket{-\ -\ -}
\end{equation}
を作るにはCNOTゲートとアダマールゲートHを使った以下の回路を実行すればよい。

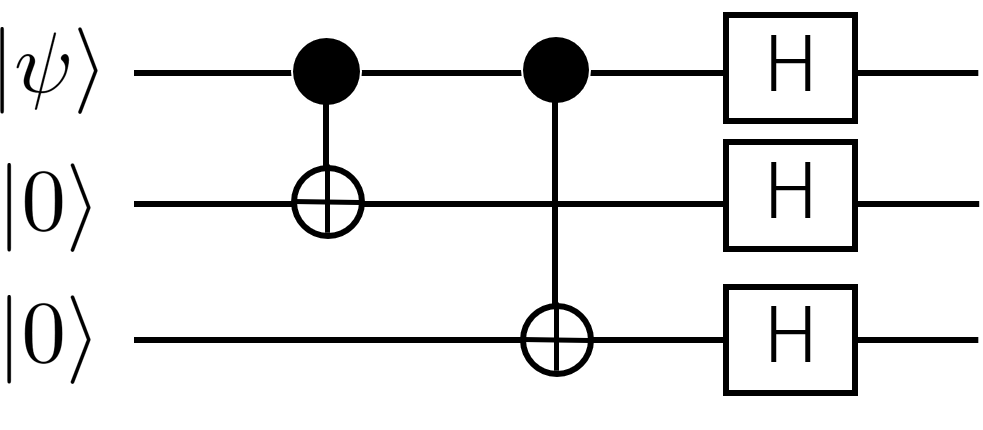
高々1ビットまでの誤りが起こるとすると、誤りのパターンはビット反転誤りの例のときと同じく誤りなしの1通りと、1ビット誤りの3通りの合わせて4通りある。誤りのパターンを特定するために、ビット反転誤りのときと同じくパリティ測定を行う。ここではパリティ測定$P$は
\begin{equation}
P = (\Ket{++}\Bra{++} + \Ket{- \ -}\Bra{- \ -} ) – (\Ket{+\ -} \Bra{+ \ -} + \Ket{- +} \Bra{- +})
\end{equation}
と$\{ \Ket{+}, \Ket{-} \}$の基底で行う。ビット反転誤りのときと同じくパリティ測定を2回行えば4パターンのうちのどれかが特定できる。対応表は以下の通りである。

位相反転しているビットが分かれば、Zゲートを作用させることで$-\Ket{1}$を$\Ket{1}$に戻せる。